以前、Excelのマクロを使って、データ個数に応じて高速フーリエ変換(FFT)と離散フーリエ変換(DFT)の処理を自動で切り替えるマクロを作成したのですが、Excelではデータ数が多い時など、使いにくい場合もあるので、今度は、C#でフーリエ変換部分をライブラリ(*.dll)にし、そのライブラリを使ったプログラムを作成しました。
実行ブログラムはこちら FourierTransform.zip
ソースコードは、すべてGitHubで公開しています。
https://github.com/ImagingSolution/FourierCSharp
使用方法は以下の通りです。
プログラムの実行
zipファイルを解凍すると、
FourierTransform.exe
FourierCSharp.dll
sampledata
となっていますので、FourierTransform.exeをダブルクリックして実行してください。
フーリエ変換できるデータフォーマット
データは1行あたりに1つのデータのCSVファイルとなります。
例)
1
1.30939551
1.59096344
1.820538079
1.980767038
2.06331351
2.069803727
2.01139008
1.906994542
1.780482109
1.65716389
1.560123288
1.506883103
1.506883103
1.560123288
入力データに実数部と虚数部が含まれる場合は、1行あたりに
実数部、虚数部
とします。
例)
50, 0
0, -25
0, 0
0, -12.5
0, 0
0, 0
サンプルのデータとして、ZIPファイル内の sampledataフォルダ内にいくつかCSVファイルを入れてありますので、そちらを参考にしてください。
データの読込
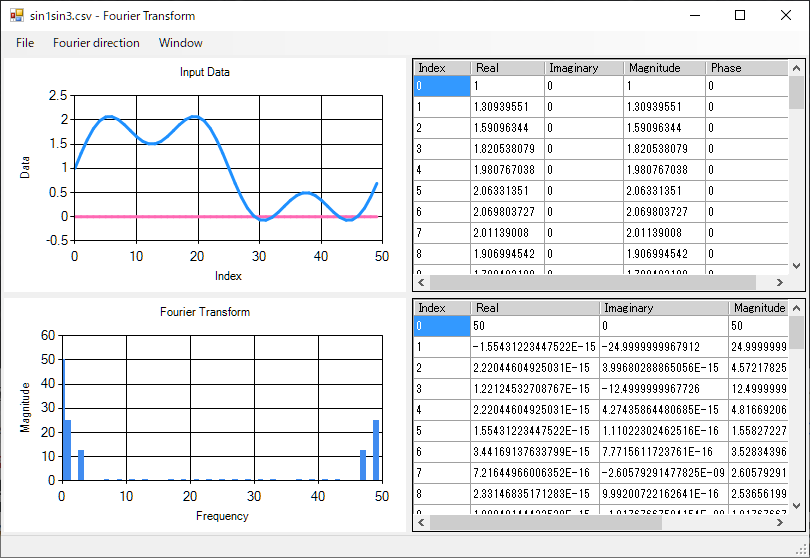
メニューの File → LoadData をクリックし、CSVファイルを指定することで、データが読み込まれ、フーリエ変換の結果(フーリエ変換後の各周波数の大きさ)が表示されます。
フーリエ変換はデータの個数が2のn乗個の場合:FFT、その他の場合:DFTを行います。
フーリエ変換、逆フーリエ変換の切替
メニューの Fourier direction → Forward もしくは Backward をクリックすることで、離散フーリエ変換、逆離散フーリエ変換が切り替わります。
離散フーリエ変換は
$$F(t)=\sum _{ x=0 }^{ N-1 }{ f(x){ e }^{ -i\frac { 2\pi tx }{ N } } } $$
逆離散フーリエ変換は
$$f(t)=\frac { 1 }{ N } \sum _{ t=0 }^{ N-1 }{ F(t){ e }^{ i\frac { 2\pi xt }{ N } } } $$
で計算しています。
窓関数
メニューの Window→ Hamming, Hanning, Blackman のいづれかをクリックすることで、それぞれの窓関数を通します。
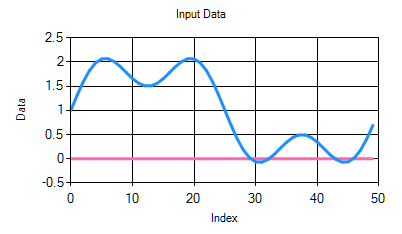 |
| ↓ 窓関数 |
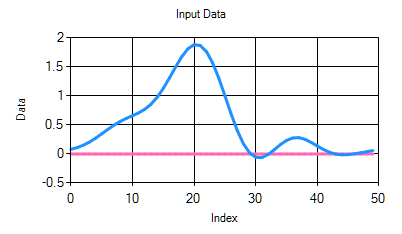 |
ただし、窓関数を通すと、元に戻せないため、元に戻す場合は、再度、データ読込を行って下さい。
免責事項
ここに公開されているプログラムは自由に使って頂いて構いませんが、バグ等による責任は待てませんので、自己責任において参照下さい。
←フリーウェアへ戻る

コメント